Si vous avez manquez les épisodes précédents :
- Episode 1 : Parlons “embarqué”
- Episode 2 : Parlons embarqué : L’heureux tour
Pour résumer, on avait parlé des opérations de bases d’un processeur et du câblage d’un boitier mémoire ridiculement petit. Un boitier de RAM, c’est bien, plusieurs boitiers, c’est mieux!
J’ai décidé aujourd’hui, en pleine semaine de solde, d’acheter un peu de mémoire flash pour mon montage, dans le but de sauvegarder les résultats de mes calculs même une fois que mes composants seront privés d’électricité (Si je vous dis que la RAM est volatile ça va ? ça ne vous choque pas ? très bien). Et comme c’était les soldes, j’ai eu le droit avec mon boitier de Flash F4k16 (4k de flash 16bit, soit 8 kilooctets de données) à un boitier de RAM M1k (rappel, 1k de ram 8bit, soit 1 kilooctet de données) offert ! Formidable !
Câblage
Nous avions vu la dernière fois que pour câbler notre boitier, nous avions du brancher 4 « catégories » de fil : le bus d’adresse, le bus de donnée, le Read/Write et le Chip Select. Pour les bus, c’est très con, on tire les fils qui vont bien. Pour la RAM, le câblage est identique à celui réalisé précédemment (10 fils, A0 à A9). Pour la flash, la plage d’adresse du boitier de flash étant plus grande (4 est supérieur à 1), il va falloir tirer plus de fils entre le processeur et le boitier. Deux de plus pour être précis. Attention, démonstration ! 4k veut dire 4096 adresses différentes, allant de 0 à 4095. 4095 en binaire vaut 111111111111. Pas la peine de compter les 1, il y en a 12. D’où mes deux fils de plus. Les esprits fins de certains lecteurs auront remarqués que je vais tenter d’interfacer un boitier avec 16bit de data sur un microprocesseur 8 bits. Ben… les promotions Carrefour étaient sur les boitiers 16 bits, que voulez vous que j’y fasse ! Déjà, c’est quoi la différence entre un boitier 16 bits et un boitier 8 bits ?
Interlude « Mathématiques, Hexadécimal et autre décalage logique ».
Je vous ai décrit la fois précédente mon boitier de ram comme un tableau Excel de 1024 lignes dont le contenu pouvait varier entre 0 et 255. Et bien le boitier 16 bit est un tableau dont les valeurs peuvent varier entre 0 et (2^16) – 1, soit 65535. On peut également le voir comme un tableau avec 2 colonnes (au hasard, on va appeler la colonne de droite LSB pour Less Significant Byte, et celle de gauche par MSB pour Most Significant Byte. Attention, en fonction du contexte, le B peut vouloir dire Bit également), dont la valeur peut varier entre 0 et 255.
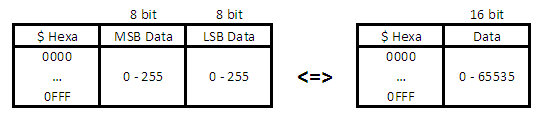
En multipliant le contenu de la case MSB par 256 et en ajoutant le LSB, on retrouve une valeur 16 bits. Pourquoi cette multiplication par 256 ? Prenons quelques exemples concrets. Et branchez votre cerveau dégourdi, on va faire des multiplications. Par deux, c’est super balèze. En binaire, 0 vaut 0 et 1 vaut 1 (si vous avez un doute, vérifiez avec la calculette de Windows, trop bien pour les conversions). 2 = 10 4 = 100 8 = 1000 Votre esprit aiguisé aura remarqué avec brio que pour passer de 2 à 4 et de 4 à 8, on dirait qu’on a juste rajouté un 0 ! Et oui, vous pouvez vérifier avec par exemple avec 3 (11) et 6 (110). La multiplication par 2 en binaire, c’est un décalage logique de 1 bit vers la gauche. Et par conséquent, une division par 2 est un décalage logique vers la droite : si on décale 14 (1110) d’un bit vers la droite, ça donne 111, soit 7. Par conséquent du conséquent, un décalage de 2 bit vers la gauche implique une multiplication par 4; 3 bit donne une multiplication par 8, etc. Alors what iz ze point avec mon boitier 16 bit ? Et bien votre MSB représente la partie 8 bit haute de votre nombre 16 bit. Elle est donc décaler de 8 bit, et donc est multiplier par 2^8 = 256. Ainsi, si votre MSB vaut 255, que votre LSB vaut 255, votre nombre 16 bit vaut 255 x 256 + 256 = 65535.
Retour à mon montage
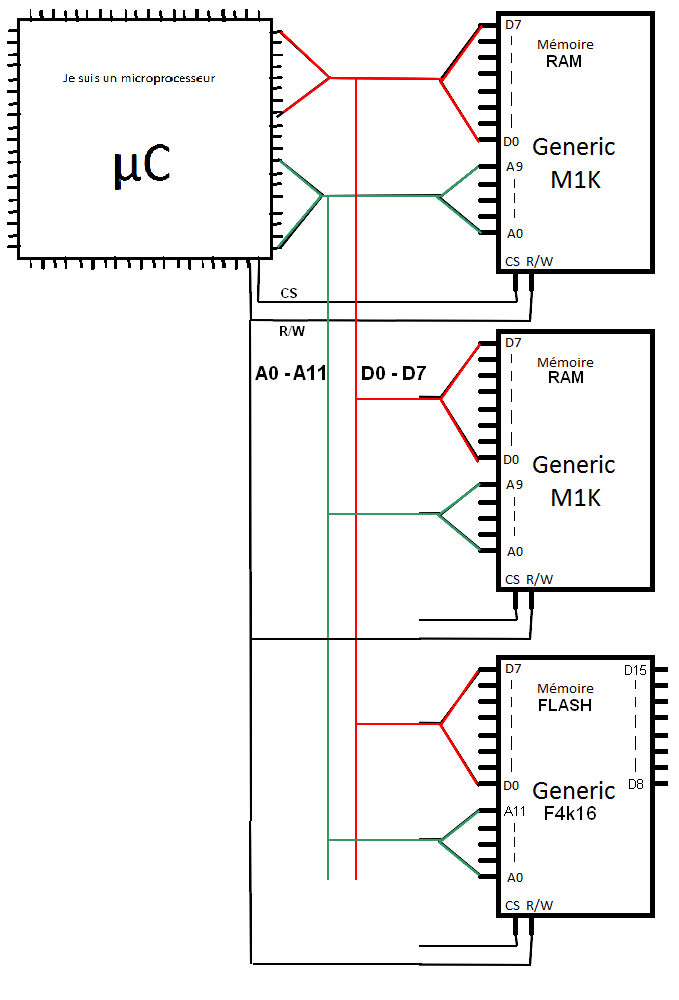
Sur le schéma, on voit que j’ai câblé les fils D0 à D7, soit ma colonne « LSB ». Je vais donc pouvoir y accéder sans problème comme sur le boitier de RAM. Pour le MSB (fils D8-D15), je ne vais rien en faire, puisque de toute façon, j’ai un microprocesseur 8 bit (enfin en vrai je vais les câbler à la masse pour éviter les perturbations de signaux mais ce n’est pas le sujet). Vous avez donc compris que je vais gâcher la moitié de la mémoire flash car je ne pourrais en l’état pas y accéder, ni en lecture ni en écriture. Mais puisque je vous dis que c’était les soldes ! Il me reste donc 2 signaux à caser : R/W et CS. R/W peut se câble comme un bus, directement sur chaque composant. Par contre pour CS, c’est un peu plus siouxe.
La source de CS (ce titre de paragraphe n’est là que pour faire monter mes stats Google)
Si vous vous rappelez de l’article précédent (c’est le cas j’en suis sur), vous savez que le CS permet au processeur de désigner à qui il s’adresse, pour qui sont destinés les valeurs qui transitent sur les bus de donnée/adresse. Et manque de bol, je viens de regarder dans la documentation technique (datasheet) du processeur, je n’ai qu’un seul sortie CS ! OMG LOL WTF §§!! Je ne peux pas utiliser le même signal CS sur mes trois boitiers puisque dans ce cas, j’écrirais dans les trois boitiers en même temps, mais surtout la lecture va se faire également en même temps et la si un boitier veut coller 5Volts sur le bus (pour écrire un 1, je rappelle) et que l’autre veut mettre 0 Volts (pour écrire un 0) ça va faire un sacré bordel. Comment vais-je donc faire ? Et bien je vais faire du décodage d’adresse. Qu’est ce que donc ?
Définir le mapping mémoire
Dans un premier, on prend un papier et un crayon, et on organise son merdier. J’ai 2 boitiers avec 1024 adresses, et un boitier avec 4096 adresses. Mon micro, lui, avec son bus d’adresse 16 bit, peut adresse 2^16 soit 65536 adresses différentes. En gros, va falloir organiser les trois plages des boitiers dans l’espace adressable total du µC. Mon premier choix, c’est de dire : j’aligne tout. D’ailleurs c’est tellement une bonne idée que je vais la garder. On n’a qu’à dire que les 1024 premières adresses sont pour le premier boitier de RAM, les 1024 suivantes pour le deuxième boitier, et les 4096 suivantes sont pour la flash. En résumé :
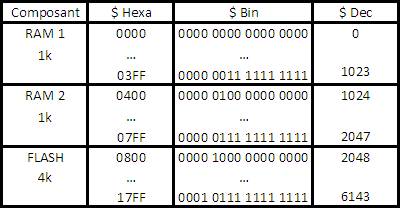
J’ai maintenant une idée de ce que je veux obtenir, je peux ENFIN passer à la gestion de mon Chip Select.
Le décodage d’adresse
Ce qui va faire la différence entre les datas qui vont dans RAM1, RAM2 et Flash, c’est la plage d’adresse que j’ai attribué à chaque composant. Je vais donc me servir de mon bus d’adresse et d’un peu de porte logique pour faire la différence entre les boitiers, j’activerai alors le CS de chacun des boitiers de façon indépendante.
Rappel de logique combinatoire (oui, on en voit des choses aujourd’hui!)
Principe de base : combiner des signaux électriques pour réaliser des opérations logiques. Les briques de bases qui vont nous servir aujourd’hui (il y en a d’autre) sont la porte ET (symbole logique « . », symbole informatique « & »), la porte OU (symbole logique « + », symbole informatique « | ») et la porte NON (symbole logique « / », symbole informatique « ! »). Vous rentrez un ou plusieurs signaux sur les entrées, et vous obtenez un résultat de l’autre côté. On appelle « table de vérité » le principe de comportement de la porte.
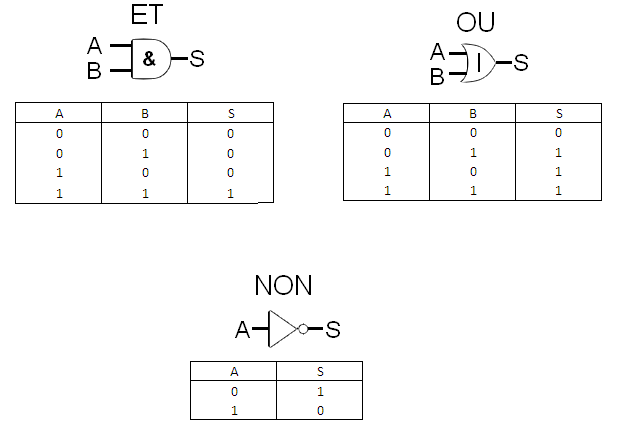
Alors pourquoi je parle de ça ? Et bien simplement car grâce à plusieurs portes logiques bien placées, on va pouvoir réaliser une « équation logique » qui va permettre de diriger notre signal CS (oui, je rappelle qu’au départ on parlait de lui, avant que vous ayez eu cette idée stupide d’écrire tl;dr). Si on regarde le mapping mémoire, en particulier les bits de poids fort (les plus à gauche), on voit que les combinaisons qu’ils composent sont propres à chaque composant. Si les bits A10, A11, A12, A13, A14 et A15 sont à zéro, on est sur d’être sur la plage mémoire de RAM1. Puis avec A10 à 1 et A11-A15 à 0, on est sur d’être sur RAM2. Pour le boitier flash, c’est un peu plus tordu car il occupe un nombre plus important de combinaison de A10-A15, mais il existe tout un art concernant la simplification d’équation logique. Nous allons les écrire vite fait, présenter le câblage de notre « décodeur ». Nous cherchons à couper notre CS en trois signaux pour chacun des boitiers : CS1 pour RAM1, CS2 pour RAM2 et CS3 pour la flash.
CS1 = CS.(/A10./A11./A12./A13./A14./A15) : pour activer CS1, il faut avoir CS à 1, et tout les autres à 0
CS2 = CS.( A10./A11./A12./A13./A14./A15) : pour activer CS1, il faut avoir CS à 1, et tous les autres à 0 sauf A10
CS3 = CS.( (/A10. A11./A12./A13./A14./A15) + (A10.A11./A12./A13./A14./A15) + (/A10./A11.A12./A13./A14./A15) + (A10./A11.A12./A13./A14./A15) ) je vous laisse comprendre, comparez ça au mapping un peu plus haut.
Voici donc notre circuit logique qui va nous produire nos trois Chip Select différents. Il sera donc impossible d’adresser en même temps deux composants.
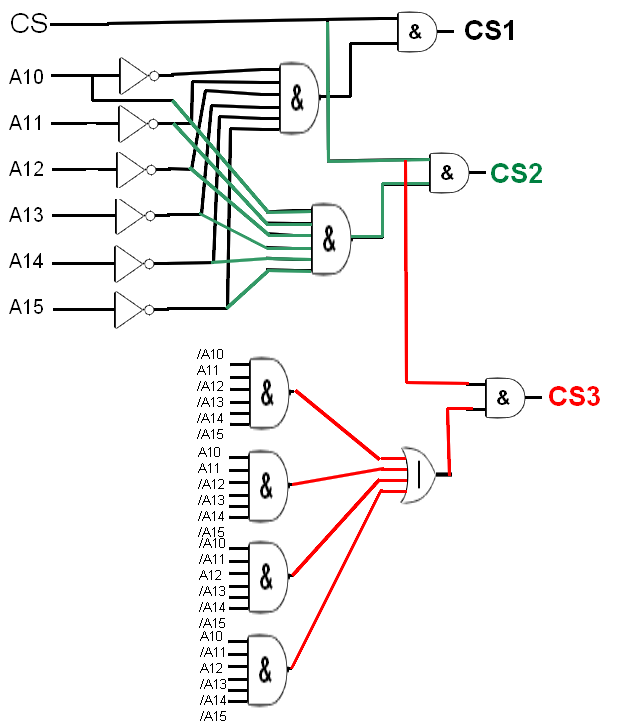
Cependant, il faut être franc, il existe en général des boitiers programmables ou ce genre de boulot, vous simplifiant clairement la tâche. D’ailleurs j’en ai trouvé un par terre, je vais tout de suite le mettre sur mon schéma final !
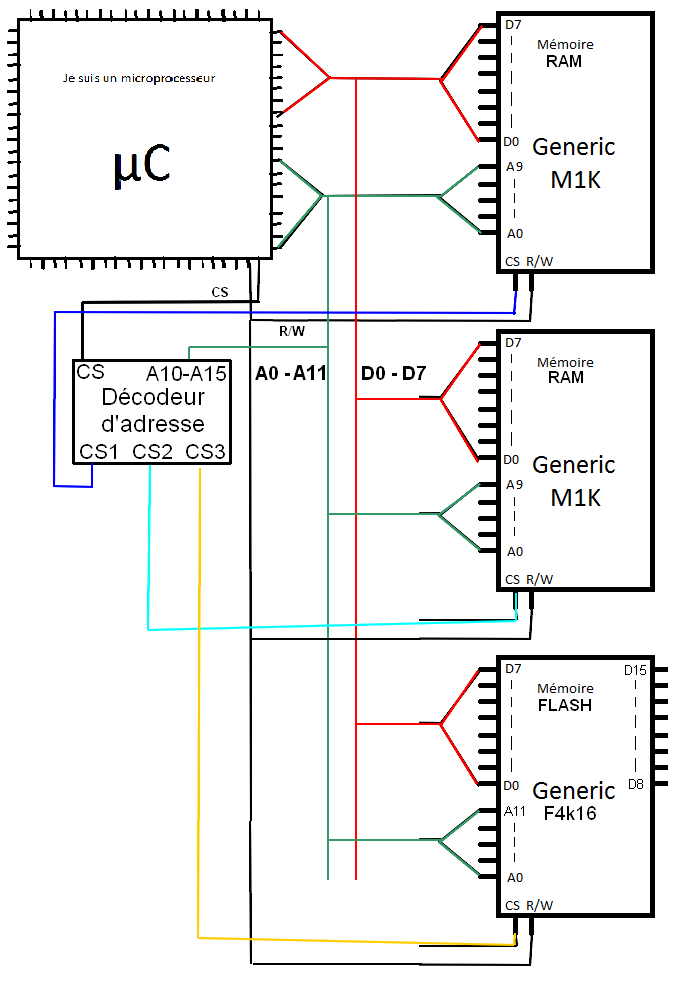
Voilà, on a encore amélioré notre système embarqué. Vous collez ça avec un alim au fond d’une machine à laver, et vous avez un système capable de :
- Charger des data qui viennent de la mémoire flash
- Faire des calculs
- Ecrire les résultats dans une mémoire externe deux fois plus grande que la dernière fois
- Faire plein de sauvegarde en flash
Il ne lui manque plus qu’un brin de communication, mais je me le garde pour plus tard. Vous devez déjà bien avoir la gerbe après avoir lu tout ça !